A taxonomy of 4x4 patterns
A TAXONOMY OF 4 X 4 tiles of 1 bit per pixels, according to symmetries. What symmetries am I counting?
- inverse of colors
- horizontal flip
- vertical flip
- 90 degree rotations.
- wrap-around offsets of the pixels (2 and 1 pixels, up and down making this 4 total mutations)
- the above in every possible combination
- sorted by the unique results.
first up, there’s two patterns that yield only two unique results after undergoing all of the above. Checkerboard, and pure black/white.
for the purposes of encoding an image, and we like variable width codes, the best way to do this seems to be to stick with the maximum width being “a code”, with smaler widths secretly being one big width code representing semantically, two or more smaller codes, this might be equivalent to huffman?
file:///Volumes/dev/organised/4x4%20experiments/enumerate256b.html
how enumeration works
- enumerate every 4x4 1bit plane (65536).
- for each, apply the permutations: hflip, vflip, rotate90, invert, in each of the 16 possible combinations.
- associate all the resulting combinations with a sequential index
- 3a. optionally index “palindromic” patterns that match one or more permutations of themselves.
- add all the resulting combinations to a set of 1-bit planes that will now be skipped and not tested.
- call the resulting set BP, with each sequential index being associated with a related set of permutations. the canonical permutation for each item in BP is the one with the lowest numerical value.
- produce a reverse lookup to find the canonical representation for any 16-bit number, plus the 4 bit hvri number needed to transform the canonical to the supplied.
- for each {BPi,BPi,BPi} set:
- For each resulting image, remap 0-7 in every permutation.
- permute every combination of HVRI,HVRI,HVRI
- take resulting set and apply a sequential index called 3BPi
- and the resulting permutations to a list of {BPi,BPi,BPi} that will not be checked, skipped.
the one with the lowest numerical value. 6. produce a reverse lookup to find the canonical representation for any 16-bit number, plus the 4 bit hvri number needed to transform the canonical to the supplied. 7. for each {BPi,BPi,BPi} set: 8. For each resulting image, remap 0-7 in every permutation. 9, permute every combination of HVRI,HVRI,HVRI 10, take resulting set and apply a sequential index called 3BPi 11, and the resulting permutations to a list of {BPi,BPi,BPi} that will not be checked, skipped.
numbers to the right = 16 symmetry group ids.
ID calculated by the lowest hexidecimal numeric value of the tiles in the group, when a tiles’ bitpatterns are converted to numbers.

 0000
0000
2

 5a5a
5a5a
2

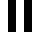

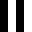 0F0F
0F0F
4
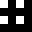

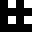

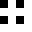
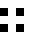

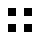 0505
0505
8







 36c9
36c9
8, 36c9


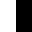
 00FF
00FF


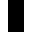
 0FF0
0FF0
8, 00FF

 33cc
33cc 
 6996
6996



 3cc3
3cc3
8, 33cc



 3c3c
3c3c



 5aa5
5aa5
8, 3c3c


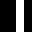

 00F0
00F0







 000F
000F
16
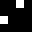
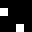
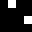





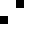
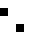
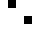
 0104
0104 








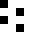

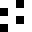



 0208
0208 
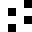
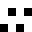
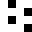 050A
050A
16 16


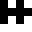


















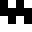










16, 05F5 16. 05FA



 2184
2184 






 1842
1842 


 1A4A
1A4A



 1842
1842 






 1248
1248 


 2585
2585
16 16



 174d
174d 





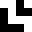
 174d
174d 


 1e1e
1e1e



 1d47
1d47 






 1d47
1d47 


 2d2d
2d2d
16 16
1 pixel, every configuration







 0001
0001




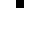
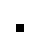
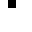
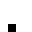 0002
0002







 0002
0002







 0020
0020
32
2 pixels in every configuration.








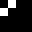








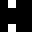

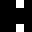
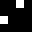
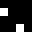





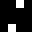















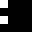

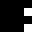

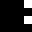
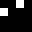

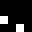
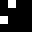



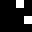
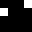










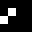

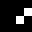





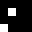





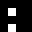

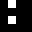

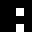

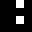

























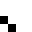

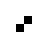





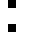

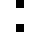
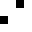
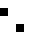
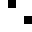


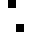

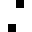






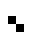



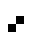
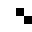





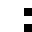

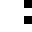
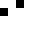
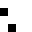

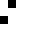
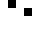
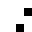

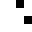








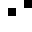


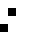

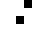

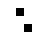
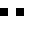
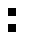
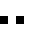
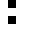

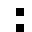

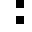








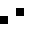
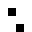
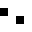
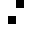
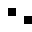
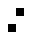
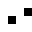
















 0003
0003




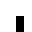
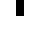
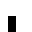
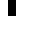







 0022
0022







 0060
0060




















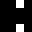
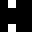
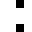
selection of 4096 tiles

center mask, all symmetries.

center mask, no shifting.

corners masking, high symmetry

corners no shift symmetry
hamming pattern

xor masking the 2x2 patterns to find sets

in other word, xor masking doubled 2x2 patterns on these 4x4 patterns can produce every other pattern.

Hamming distance of 1 from each progressive tile
removed from occurring in the rest.
in other words, each tile cannot have

same but with shifting symmetries added in. is there a difference?

hamming distance 2 eliminated

hamming 2 with xor masks




partially sorted by hand

only flipping and inversion

from the other category, some interesting groups






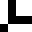
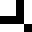
L: 8 o: 1e22 i: 279
















L: 8 o: 1e2a i: 280








L: 8 o: 71f i: 124
one of the many x256 groups










































































































































































































































I’ve clearly screwed something up. there’s duplicates here.











